MC Control: Constant-alpha

In an earlier quiz (Quiz: Incremental Mean), you completed an algorithm that maintains a running estimate of the mean of a sequence of numbers (x_1, x_2, \ldots, x_n). The running_mean function accepted a list of numbers x as input and returned a list mean_values, where mean_values[k] was the mean of x[:k+1].

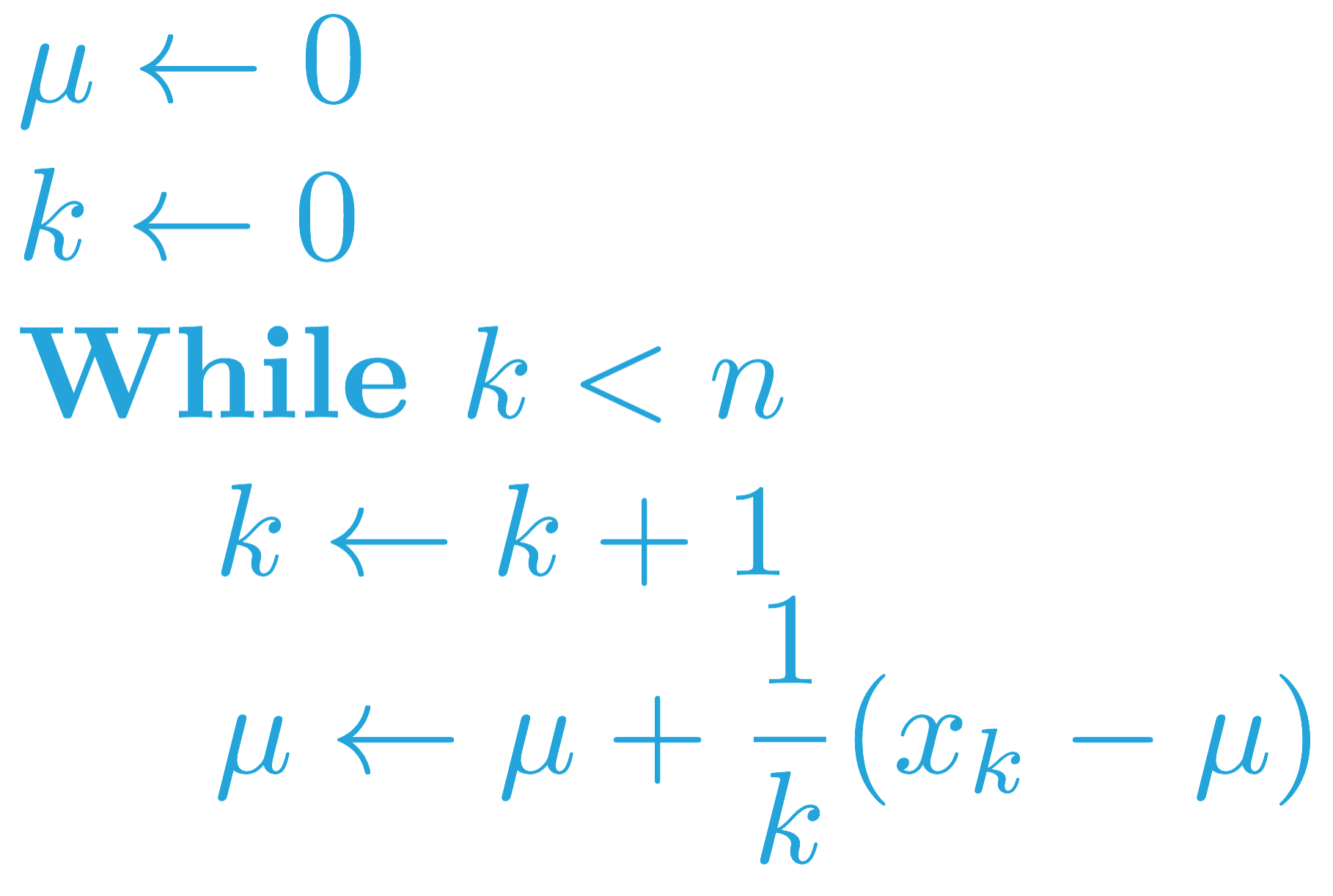
When we adapted this algorithm for Monte Carlo control in the following concept (MC Control: Policy Evaluation), the sequence (x_1, x_2, \ldots, x_n) corresponded to returns obtained after visiting the same state-action pair.

That said, the sampled returns (for the same state-action pair) likely corresponds to many different policies. This is because the control algorithm proceeds as a sequence of alternating evaluation and improvement steps, where the policy is improved after every episode of interaction. In particular, we discussed that returns sampled at later time steps likely correspond to policies that are more optimal.

With this in mind, it made sense to amend the policy evaluation step to instead use a constant step size, which we denoted by \alpha in the previous video (MC Control: Constant-alpha, Part 1). This ensures that the agent primarily considers the most recently sampled returns when estimating the action-values and gradually forgets about returns in the distant past.

The analogous pseudocode (for taking a forgetful mean of a sequence (x_1, x_2, \ldots, x_n)) can be found below.

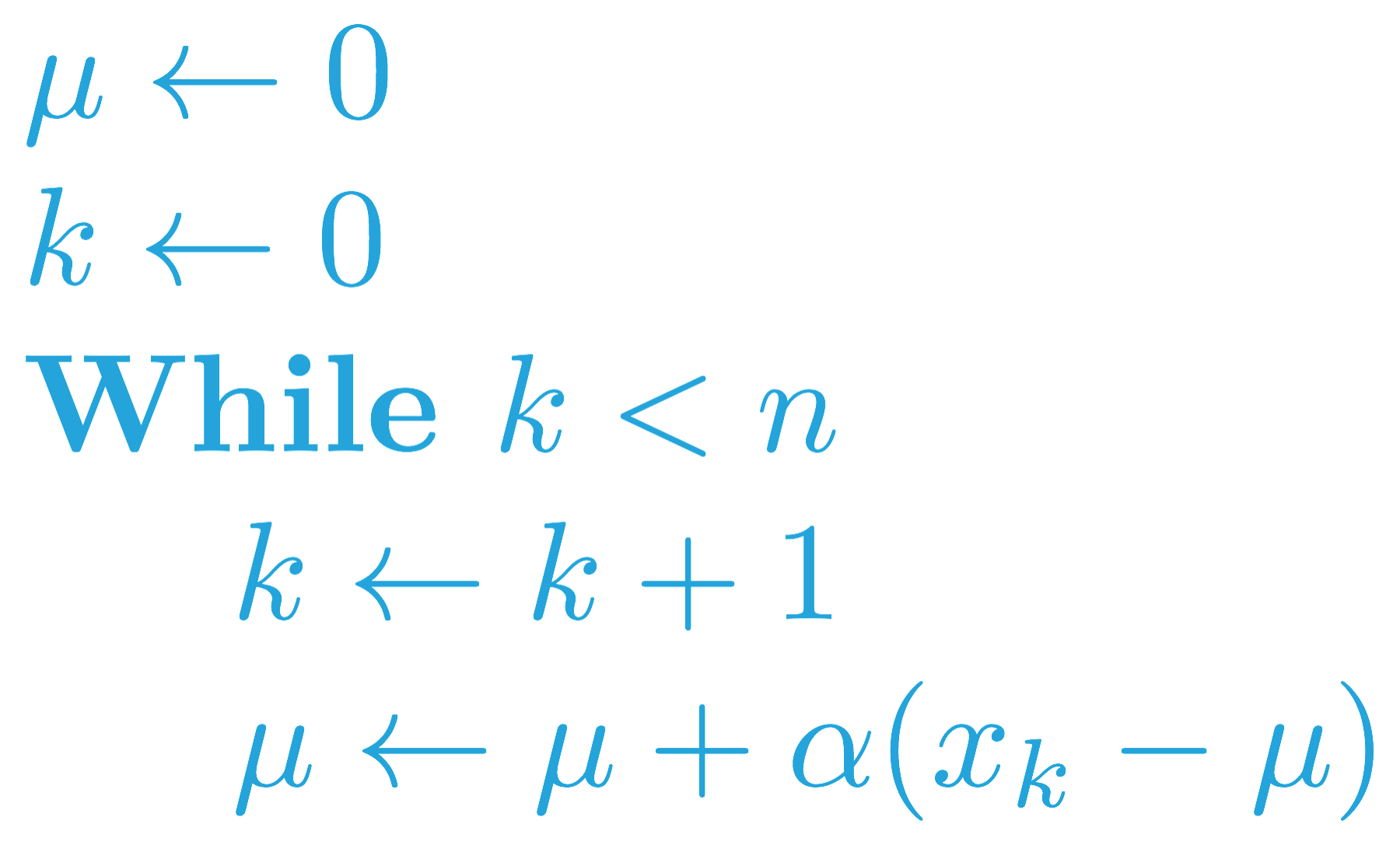
This change has been implemented in the forgetful_mean function below. The function accepts a list of numbers x and the step size alpha as input. It returns a list mean_values, where mean_values[i] is the (i+1)-st estimated state-action value.

The print_results function analyzes the difference between the running_mean and forgetful_mean functions. It passes the same value for x to both functions and tests multiple values for alpha in the forgetful_mean function.

Take the time to become familiar with the code below. Then, click on the [ Test Run ] button to execute the print_results function. Feel free to change the values for x and alpha_values, if you would like to run more tests to further develop your intuition.

Start Quiz:

quiz.py

import numpy as np

# This is the sequence (corresponding to successively sampled returns). 
# Feel free to change it!
x = np.hstack((np.ones(10), 10*np.ones(10)))

# These are the different step sizes alpha that we will test.  
# Feel free to change it!
alpha_values = np.arange(0,.3,.01)+.01

#########################################################
# Please do not change any of the code below this line. #
#########################################################

def running_mean(x):
    mu = 0
    mean_values = []
    for k in np.arange(0, len(x)):
        mu = mu + (1.0/(k+1))*(x[k] - mu)
        mean_values.append(mu)
    return mean_values
    
def forgetful_mean(x, alpha):
    mu = 0
    mean_values = []
    for k in np.arange(0, len(x)):
        mu = mu + alpha*(x[k] - mu)
        mean_values.append(mu)
    return mean_values

def print_results():
    """
    prints the mean of the sequence "x" (as calculated by the
    running_mean function), along with analogous results for each value of alpha 
    in "alpha_values" (as calculated by the forgetful_mean function).
    """
    print('The running_mean function returns:', running_mean(x)[-1])
    print('The forgetful_mean function returns:')
    for alpha in alpha_values:
        print(np.round(forgetful_mean(x, alpha)[-1],4), \
        '(alpha={})'.format(np.round(alpha,2)))

Setting the Value of \alpha

Remember that the forgetful_mean function is closely related to the Evaluation step in constant-\alpha MC control. You can find the associated pseudocode below.

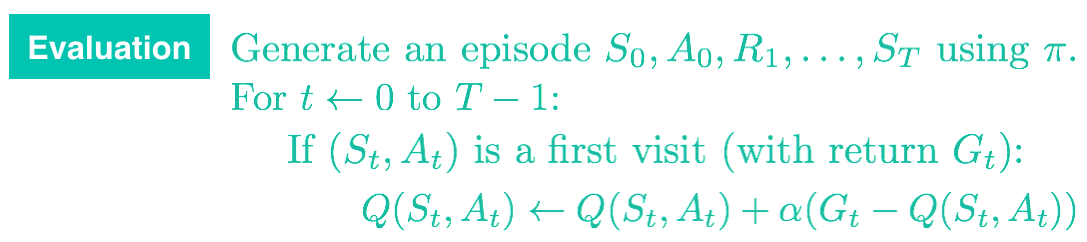
Before moving on to the next concept, use the above coding environment to verify the following facts about about how to set the value of \alpha when implementing constant-\alpha MC control.

You should always set the value for \alpha to a number greater than zero and less than (or equal to) one.
- If \alpha=0, then the action-value function estimate is never updated by the agent.
- If \alpha = 1, then the final value estimate for each state-action pair is always equal to the last return that was experienced by the agent (after visiting the pair).
Smaller values for \alpha encourage the agent to consider a longer history of returns when calculating the action-value function estimate. Increasing the value of \alpha ensures that the agent focuses more on the most recently sampled returns.

Note that it is also possible to verify the above facts by slightly rewriting the update step as follows:

Q(S_t,A_t) \leftarrow (1-\alpha)Q(S_t,A_t) + \alpha G_t

where it is now more obvious that \alpha controls how much the agent trusts the most recent return G_t over the estimate Q(S_t,A_t) constructed by considering all past returns.

IMPORTANT NOTE: It is important to mention that when implementing constant-\alpha MC control, you must be careful to not set the value of \alpha too close to 1. This is because very large values can keep the algorithm from converging to the optimal policy \pi_*. However, you must also be careful to not set the value of \alpha too low, as this can result in an agent who learns too slowly. The best value of \alpha for your implementation will greatly depend on your environment and is best gauged through trial-and-error.

Next Concept